Kategorien von Nutzerprogrammen
In diesem Abschnitt werden anhand von Beispielen sechs verschiedene Kategorien von Computerprogrammen vorgestellt (vgl. Girwidz 2010).
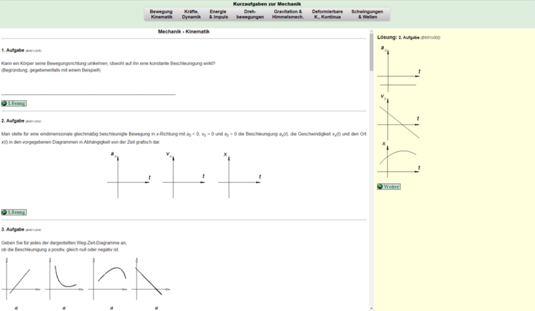
Übungsprogramme...
...stellen dem Lerner eine Aufgabe und kontrollieren den weiteren Verlauf der Übung. Sie geben Feedback, bevor sie zur nächsten Aufgabe überleiten.
Übungsprogramm mit Kurzaufgaben zur Mechanik. Zum starten bitten das Bild klicken.
Selbstlerneinheiten und tutorielle Programme...
...informieren zunächst über ein Themengebiet. Darauf folgen Verständnisfragen. Diese ermöglichen es, den Lernfortschritt zu überwachen und den weiteren Verlauf der Lerneinheit individuell anzupassen.
Computerwerkzeuge...
...entlasten den Lerner von Nebentätigkeiten (z.B. Nebenrechnungen). Die dadurch frei werdenden kognitiven Ressourcen erleichtern das weitere Lernen.
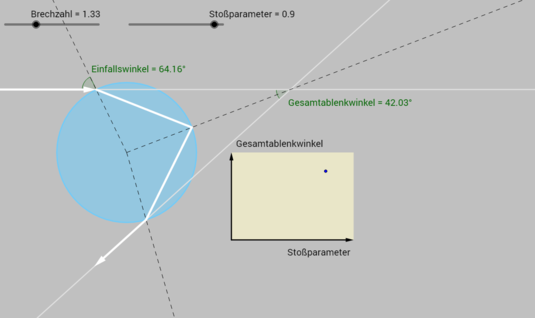
Mit Geogebra können mathematische Zusammenhänge mit relativ geringem Aufwand visualisiert werden. Der Screenshot zeigt eine Simulation zur Brechung von Licht an einem Regentropfen aus dem Buch "Optik mit Geogebra" von Roger Erb (2017). Es enthält eine Zusammenstellung unterschiedlichster optischer Phänomene, die mit Hilfe von Geogebra aufgearbeitet wurden. Zum Internetauftritt von Geogebra gelangen Sie hier.
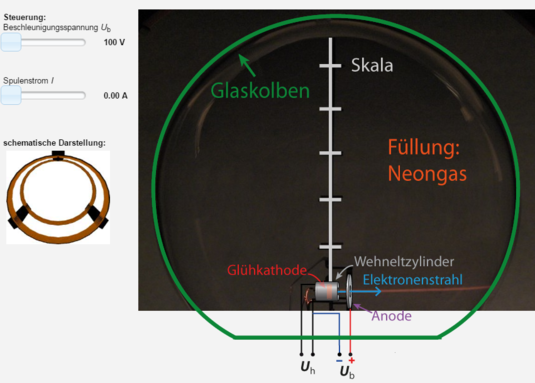
Simulationsprogramme...
...zeigen ein vereinfachtes Abbild der Realität. Lerner können Einflussfaktoren variieren und sammeln so interaktiv Erfahrungen zum Lerninhalt.
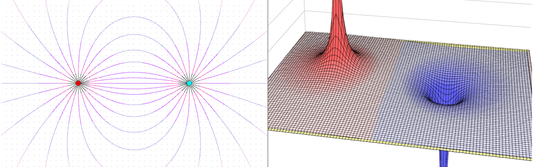
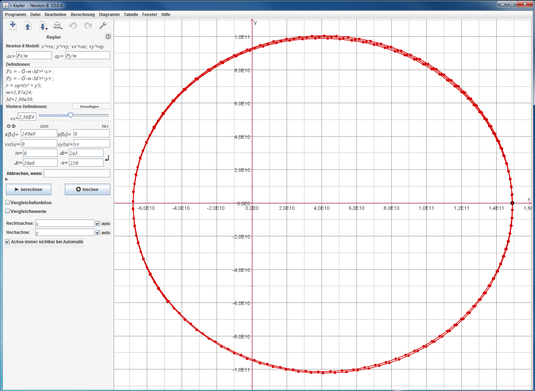
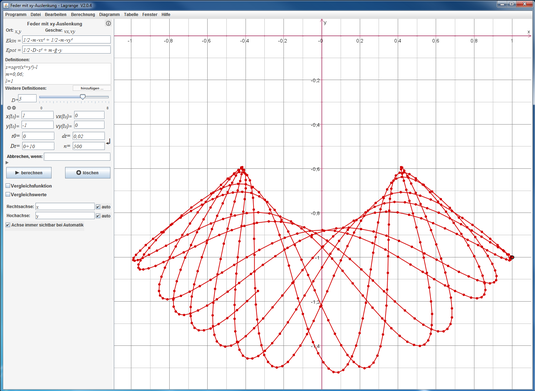
Modellierungsprogramme...
...ermöglichen ein eigenes Entwickeln und Testen von formalen Modellen zu einem Sachverhalt oder Phänomen. Es können Modellannahmen beeinflusst und zugrunde liegende Formeln verändert werden. Der Anwender bekommt so einen tieferen Einblick in die relevanten Strukturen.
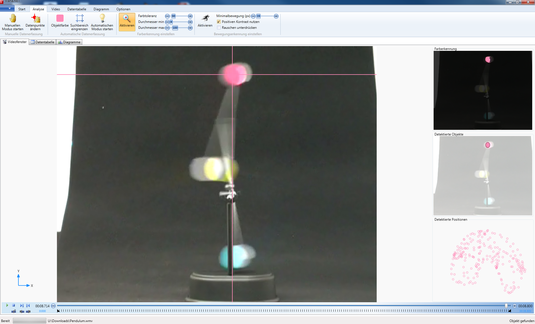
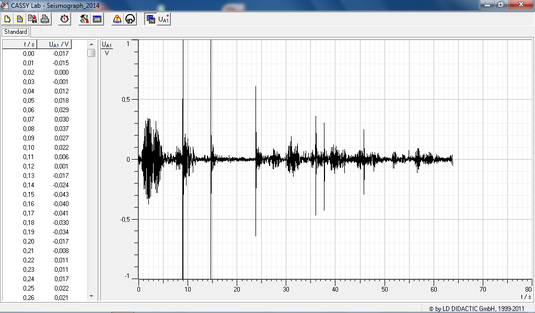
Messwerterfassungssysteme...
...erfassen automatisiert Messdaten und helfen bei ihrer Auswertung. Sie bieten oft zusätzliche Visualisierungsmöglichkeiten an.
Literaturangaben:
Erb, R. (2017). Optik mit Geogebra. Berlin/Boston: Walter de Gruyter GmbH.
Girwidz, R. (2010). Neue Medien und Multimedia. In E. Kircher, R. Girwidz & P. Häußler (2010). Physikdidaktik: Theorie und Praxis (2. Aufl.)(S.424-426). Berlin: Springer Lehrbuch.